Advanced addition and speedup of neural network evaluation
Published August 1, 2019
Hello! I've been doing some more work on the advanced addition project.
Last time, I had just created some silly neural networks that added two numbers. The evaluation was trivial, but I was able to make the simple one explainable by boiling it down to the literal equation with the two inputs. I've made progress on this front.
I was able to break down the fully connected 2-10-1 neuron network (Model C) into its respective equation. Evaluated in order, this looks something like this:
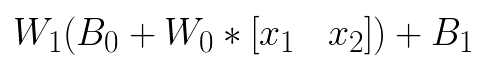
Since each variable is just a matrix of some size, and I've nicely arranged them in a way that allows multiplication, we can precompute some of the matrix multiplications for the final equation and arrive at a shortened form of the neural network for implementation purposes. You can think of this shortened form as a much easier model to evaluate for low power, discreet package sizes in remote areas without large computing pools.
The sizes of each variable are not exactly clear from this LaTeX equation, but trust me when I say its just simple matrix multiplication. Nothing fancy. Depending on the initial setup, the final equation for Model C reduces to something like this:
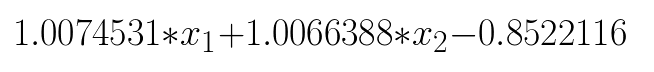
We can see that the equation is very similar to Model A's original equation from this post, despite Model C's 30 multiplications and 20 additions against Model A's two multiplications and two additions. This got me thinking; why can't we do this to every model? Why can't we precompute the matrix multiplications for every neural network, like those built for edge-computing on cameras or speakers?
I thought I was clever for a second, but then I realized that my models would only be able to approximate linear functions. The only features taken for input would be x
Activation functions could be broken down some more, but I would have to spend a little more time with it. I think that the individual nature of the function means that a simple precomputation wouldn't be allowed. We could threshold the inputs by backtracking the minimum value required to overcome the ReLU or something, and that would save a bit of time.
So, the takeaway is that most neural networks cannot be sped up using precomputation, since every layer usually has a nonlinear activation function. But in any model with multiple matrix multiplications or additions done in succession, the evaluation of the two matrices can be precomputed to speed up the model.