Real Time Fourier Transform Using Shaped Aperture
Published September 20, 2021
Hello! I'm going to tell you something cool about light. Specifically, how to use apertures and lenses to perform the Fourier Transform of a 2D image at the speed of light.
Backstory
When I was still a wee boy, my computational photography professor mentioned that a lens performs a Fourier Transform on light that enters it. A Fourier transform of light is a frequency domain representation of the image, and captures the exact same information as the regular picture. We don't usually notice this property of lenses because it only happens to coherent light, like a laser. One example of this is how a bright image (the sun) becomes a single point at the focus of the lens, because there is a 0-frequency component to the brightness entering the lens.
Example Fourier Transform of an image, specifically showing a text rotation application (source)
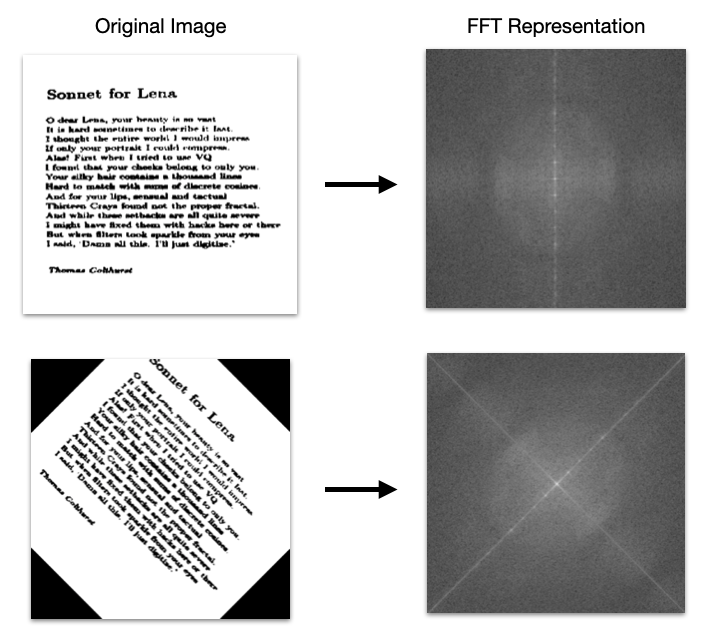
Anyway, I noted this cool fact and carried on with my life
1 Year Ago
About a year ago, I bought a coffee table book called "Laser Art and Optical Transforms", by a Mr. Thomas Kallard. The book contained a ton of photos of interesting laser effects that the author had created over his career as a lighting designer, and were catalogued down to the equipment he had used to make them.
A copy of the book, mine is black

I read the whole book (looked at pictures), and noticed that the back half of the book was entirely these aperture pictures.
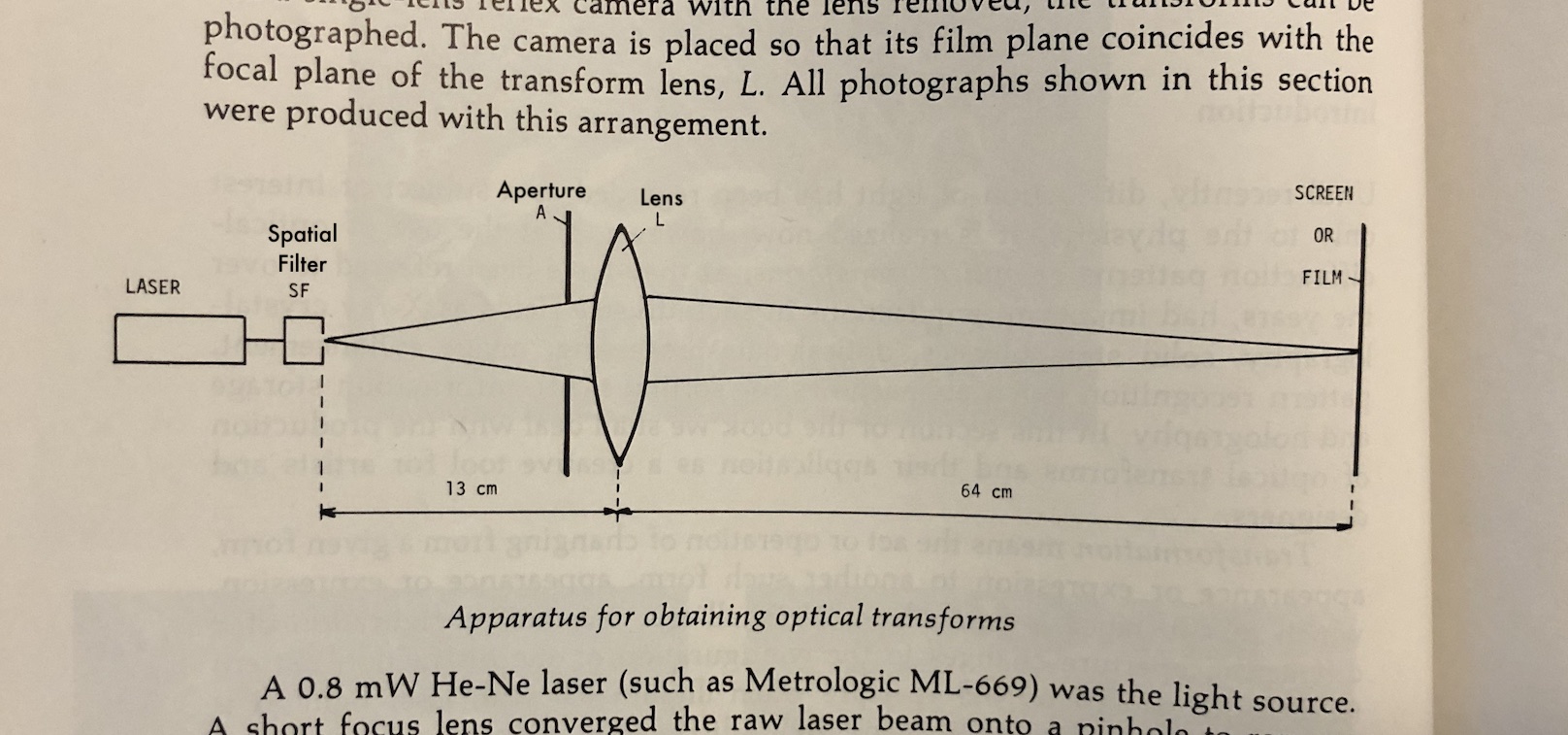
To make these aperture photos, Kallard took a laser beam that was spread out by a filter, then shot through a sheet of paper with a shape cut out. The resulting image on the far wall did not resemble the hole at all, due to the self-interference of the laser light shooting through the paper cut-out. If the light source were an incoherent light source like a lamp or projector, this resulting image would look very different, but we don't have to worry about that since Mr. Kallard did use a laser.
Mr. Kallard's setup
Here's an example from the book, showing how changing the laser aperture shape changes the resulting image. The transform is slightly intuitive, but this reasoning breaks down with more complex apertures.
Two dots vertically stacked make a circle with horizontal lines, two dots stacked top right and bottom left create a circle with diagonal lines.

Last Week
I showed a friend my book, and he wondered aloud how the output images were being formed by the light's interference. Using what I learned from computational photography, I assumed that this was a similar principle, and that changing the aperture and changing the "image" coming into a lens were nearly the same thing. This would mean that the aperture pictures that Kallard had captured were probably just the Fourier Transforms of the apertures he was using.
I had never tried it myself, but in that moment I remembered this web-based Fourier Transform demo I had found that let you do your own images. In a flash, we had taken a few photos of the apertures and fed them into the web demo. Lo and behold, what should we find but near-matches to the actual output Kallard had recorded!
1. Circles
Here's some overlapping circles. The left image is the shape of the laser aperture, and the top-right image is the output that Kallard photographed. You can see the X and the overlapping arcs that face opposite directions on both, but the scale of the image is the only thing that changes.
Circle aperture + FFT

2. Spiral-y thing
Similarly here, it's clear that the aperture on the left creates features like the 4 bright quadrant and the surrounding "fan" shapes in both the web and real world version, though they are a bit harder to see.
Spiral aperture + FFT

Kinda crazy! I'm surprised that taking the FFT of a photo worked so well, considering that the photo has all sorts of distortion and noise from the paper warp and real world effects.
I'm still not sure why the scale of the image was so zoomed for Kallard's images. The spread of the light depends on your angle, and Kallard had quite a large distance between his lens and the photographing wall. Perhaps if you were to recreate this using a closer camera, you'd get the same thing we got.
Either way, pretty dope.