Oversampling vs. Averaging for Noise Reduction
Published January 24, 2021
Hi! Today I was curious about the effects of oversampling a single, high sample frequency channel of data vs 4 simultaneously sampling channels of the same data, and which would give better data. This ties into my work on EEG processing, where I have the chance to use up to 4 channels but don't want to just average all of them because that seems too simplistic.
What did I try then?
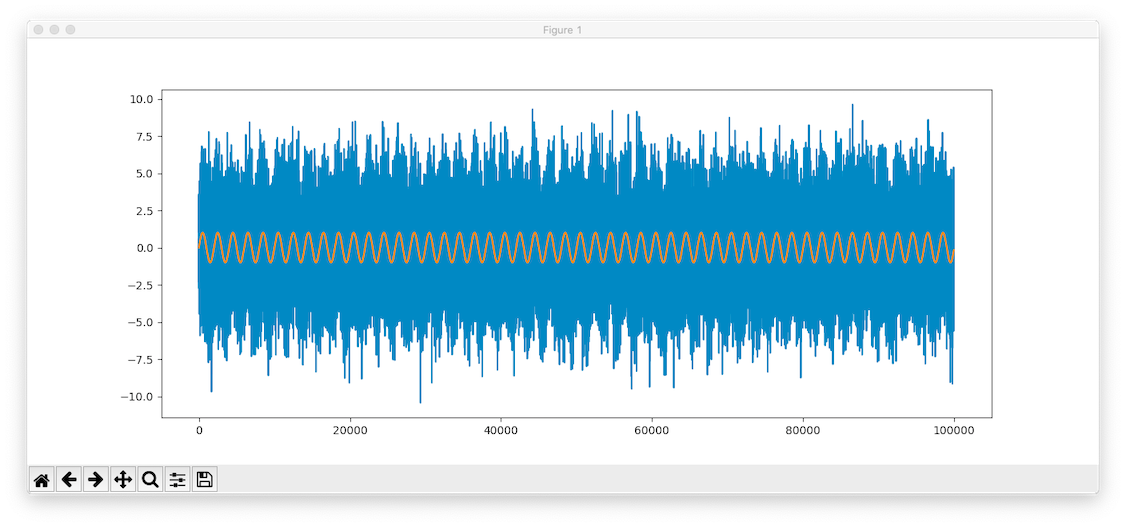
So, I generated a sine wave at a low-ish frequency (50Hz) of amplitude 1, then added Gaussian noise of power 10 to it. It has duration 1 second, but I created it using a 100kHz "sample frequency". Here's what it looks like.
Graph of the original and corrupted signal. Orange is the original
I then took 1 sample every n samples in order to create two downsampled data streams. One was sampled every 100 samples, giving a sample rate of 1kHz. The other took one point every 500 points, and had a sample rate of 200Hz. I then compared their FFTs.
Spectrum of the 200Hz sampled signal vs the 1kHz sampled signal. Blue is the 200Hz.
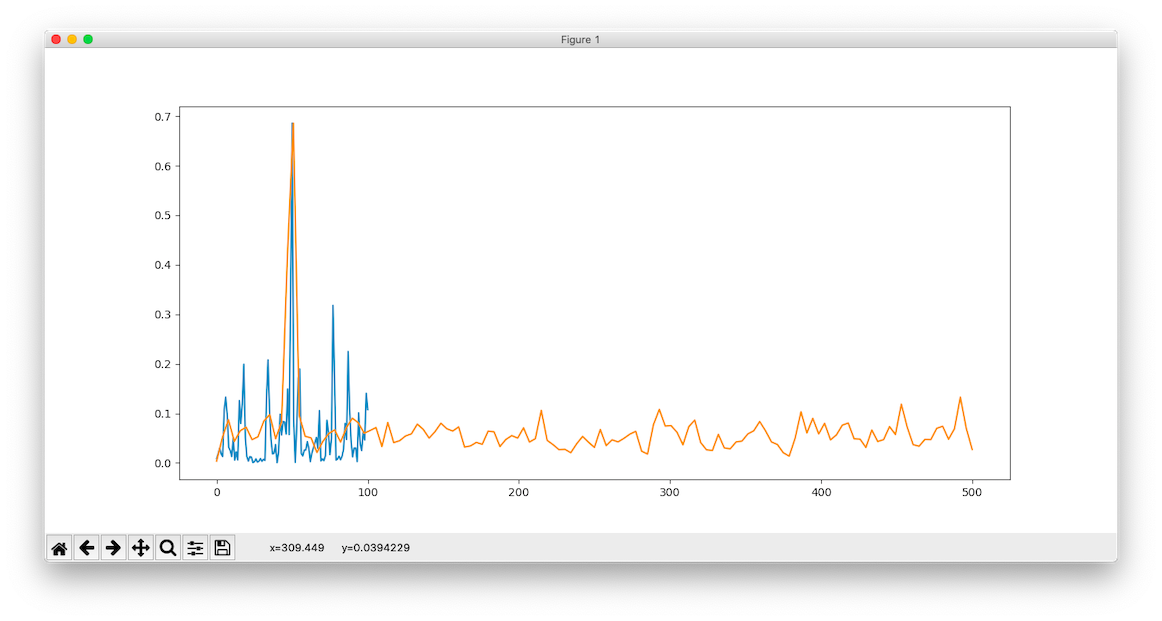
Spectrum of the 200Hz sampled signal vs the 1kHz sampled signal, zoomed in to show the difference. Blue is the 200Hz, and much noisier.
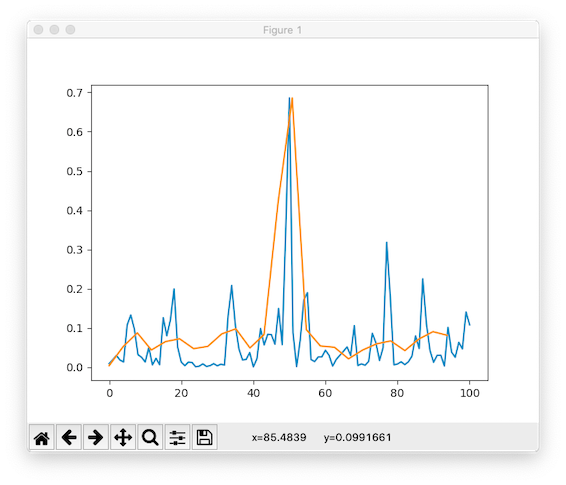
I've scaled the peaks so they line up, but we see clearly that the 1kHz signal (orange) has much lower noise compared to its peak compared to the 200Hz signal. Let's see what happens if we downsample the 1kHz signal down to 200Hz and compare spectrums then.
Blue is the 1kHz signal downsampled to 200Hz, orange is the original 200Hz sampled signal. The downsampled data is much less noisy
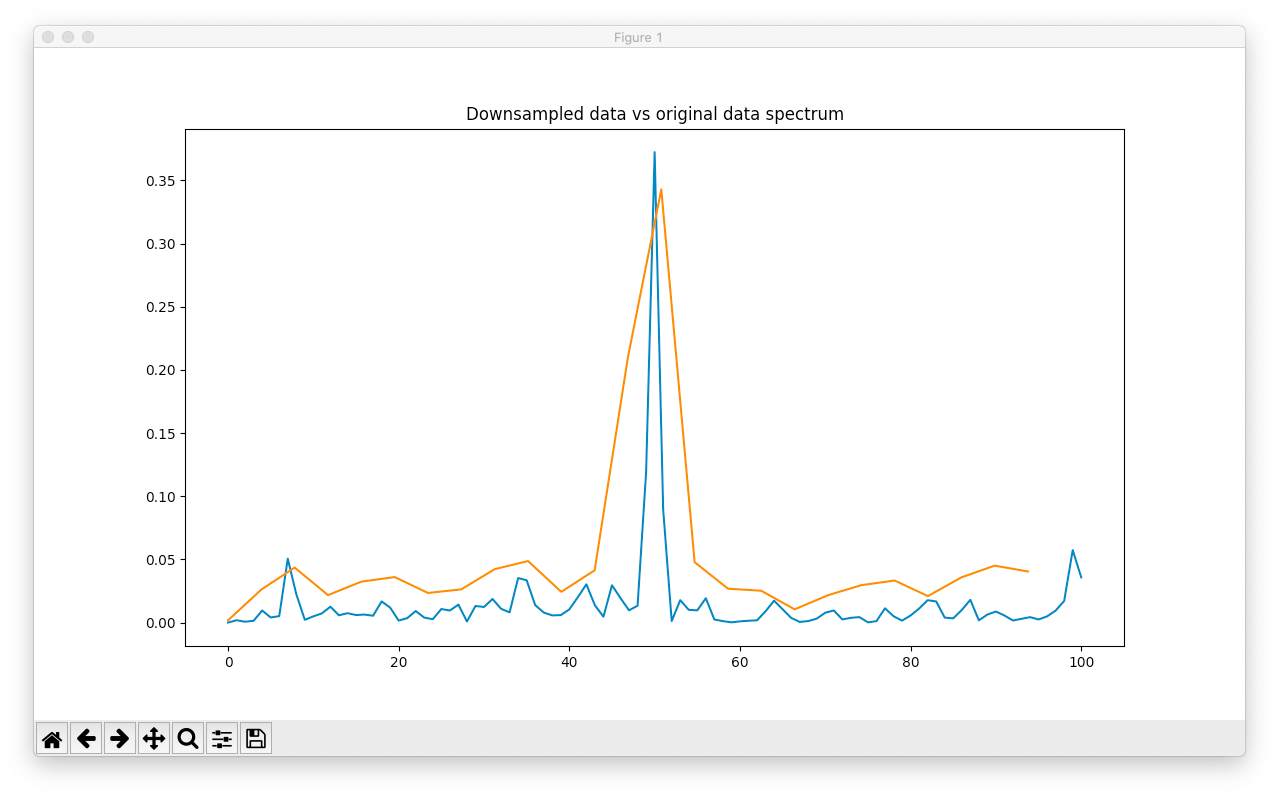
We see that the downsampled data beats the 200Hz anyway, even though they're at the same length now and sample frequency now.
What if the 200Hz sampling had 4 unique channels? These are created frmo the original 100kHz signal, and are side by side. What if they were all averaged together to reduce the Gaussian noise (simulating averaging channels)?
Blue is the 4-channel average, each 200Hz. Orange is the downsampled 1kHz spectrum.
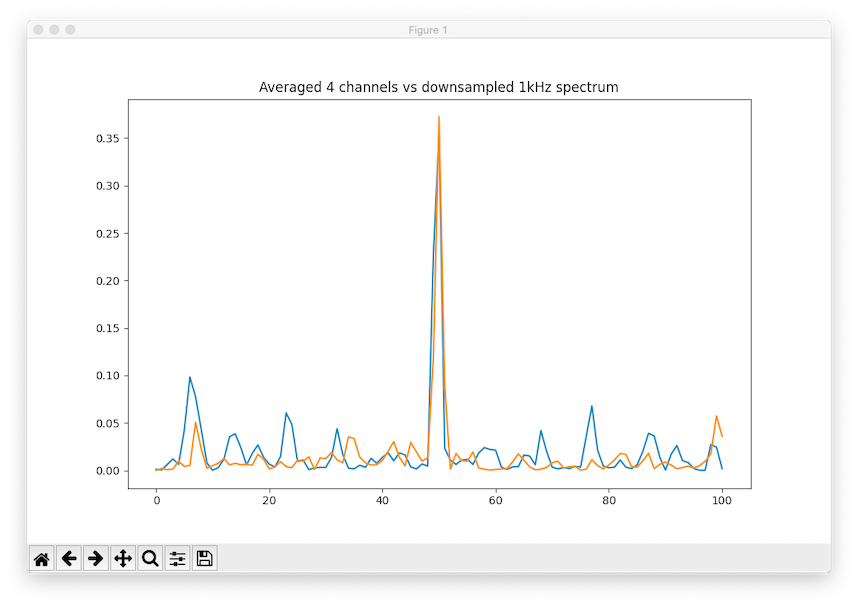
Blue is the averaged, orange is the downsampled spectrum. We see that the noise has gone down by a lot in the original 200Hz spectrum, but it's still higher than the oversampled one by about a factor of 2 (just from comparing peaks visually). Here's the same plot including the original, unaveraged 200Hz channel.
Same as the last graph, but with the original 200Hz sampled spectrum in green.
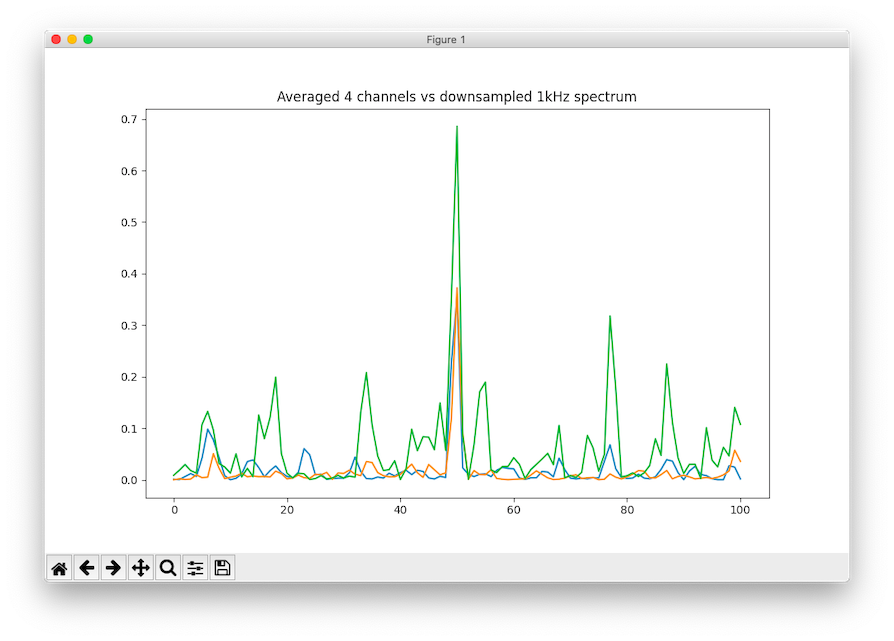
Though I didn't scale the peaks, we see that the noise power has gone down by a factor of 2 (makes sense because of the Gaussian noise), but it still doesn't beat the downsampled 1kHz data. Even if we lower the original signal frequency, the oversampled one continues to outperform the multi-channel setup.
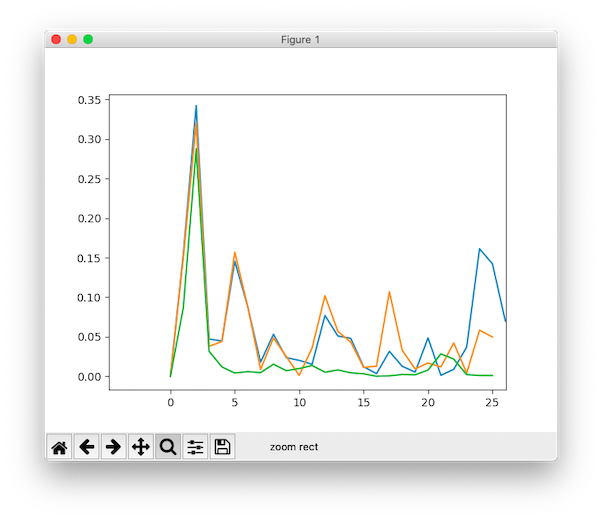
The orange is actually the averaged one here, it has higher noise peaks than the original signal.
At a lower signal frequency, the downsampled 1kHz signal still has the lowest noise (green). The averaged 4-channel signal has even higher noise than the original 200Hz signal actually (orange vs. blue).
Discussion
I didn't think the effect would be so drastic, but it seems that sampling at a high rate then downsampling is a very effective strategy compared to averaging all your channels together. But then I don't know what to do with my 4 channels then...
This result is counterintuitive because having 5, 200Hz channels and averaging them is equivalent to sampling at 1kHz and downsampling.
If we imagine a 1kHz sampled signal, what we did to generate the 200Hz signal was take 1 of every five sample points. This means if we had 5 “channels” (each offset by 1 from the beginning), then its equivalent to down sampling the 1khz signal. But it’s weird that using 4 I didn’t have nearly the same effect, and I don't expect going to 5 channels to change much.
It might be different because our 200Hz channels were taken from the original signal, which was created at a much higher sample rate (100kHz), instead of taking them frmo the 1kHz signal. But it seems like a minor difference, honestly.