Calculating the expected value of the PA scratch offs
Published February 4, 2021
Hi! Yesterday I had a dream where I won a math prize (unlikely) and received a prize of 200 million dollars (even more unlikely). I then woke up, and decided that I needed to lose 20 dollars immediately on the Pennsylvania lottery (I think the odds of this one are the most unlikely out of all three occurences).
After getting a bunch of scratch off dust all over my bedroom carpet, I ended up $20 poorer, and decided to calculate the expected value of each game I played. The website lists the chances of winning at all (usually around 1:3 to 1:5), then also has a pdf in each page that lists "Chances of Winning" for that game in particular.
A brief aside, some lotteries will show your odds instead of chances. This is SIGNIFICANTLY different. Odds are wins:losses, instead of wins/(wins+losses), which in this case would change 1:3 to 1/4.
An example "Chances of Winning" pdf from a real active game in PA as of 2/4/21
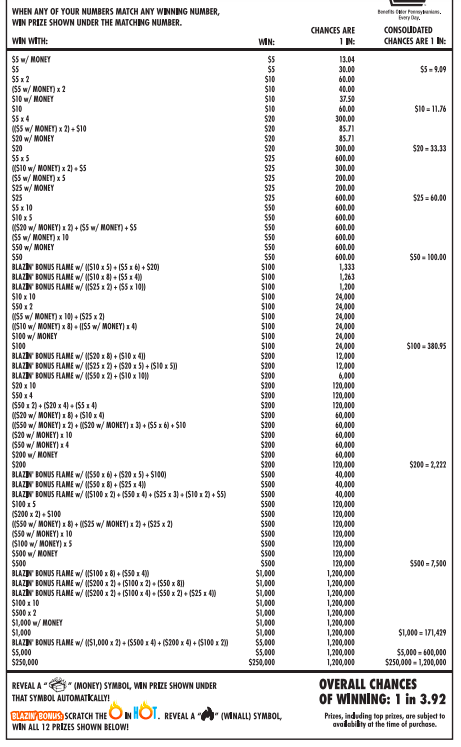
PA Lottery offers scratch-offs that cost 1, 2, 3, 5, 10, 20, and 30 dollars. I took the most recent game of each value, and added up the expected values (prize amount * probability of winning prize). I know it doesn't generalize well since I'm only using one of each cost level, but YOU try to scrape a PDF with variable rows. Have fun with that. This data was collected on 2/3/21 from the PA Lottery site.
| Scratch-Off Game | Cost | Expected Value | Net Loss | % Change |
|---|---|---|---|---|
| 3 Mil Extra | $30 | $23.10 | -$6.9 | -23% |
| 1 Mil Jack | $20 | $15.01 | -$4.99 | -25% |
| WIN WIN WIN | $10 | $7.31 | -$2.69 | -26.9% |
| Leprechaun | $5 | $3.52 | -$1.48 | -29.6% |
| Wild Cash | $3 | $1.98 | -$1.02 | -34% |
| O'Lucky Coin | $2 | $1.31 | -$0.69 | -34.5% |
| Clover All Over | $1 | $0.71 | -$0.29 | -29% |
Results seem as expected, the more you pay, the less you lose proportionally, though not in raw cash. And, of course, house always wins. The calculated chances also reflect this, with the $30 dollar games offering the highest chances of winning anything.
Weirdly enough, it seems that the loss from $1 games is the same as loss from $5 games, which makes you feel like you should buy 5x 1$ games instead of 1x 5$ game. Whatever gets you going, I guess. You lose money either way.